Encoding a magic state with beyond break-even fidelity

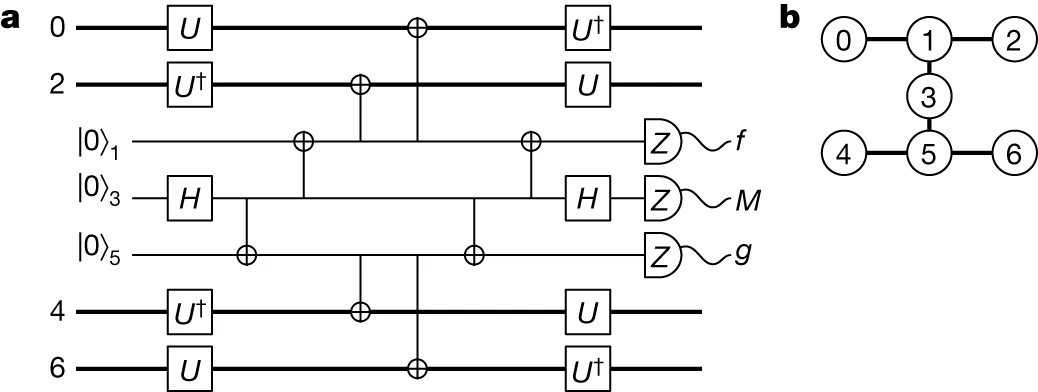
In order to run large-scale algorithms on a quantum computer, error-correcting codes play a crucial role in performing logic gates while protecting the encoded information from noise. One key aspect of achieving a universal set of logic gates involves the production of magic states, which are special resources that are essential for quantum computations. The significance of producing high-fidelity magic states cannot be overstated, as it allows for the execution of algorithms with minimal noise interference. In a recent study published in Nature, researchers have introduced a groundbreaking scheme to prepare magic states on a superconducting qubit array using error correction techniques. Remarkably, the results of this study have shown that the proposed scheme is capable of generating superior magic states compared to those produced by individual qubits within the device. This highlights an important principle in fault-tolerant quantum computing, demonstrating that error correction can significantly enhance the quality of logic gates even with noisy qubits. Furthermore, the researchers have discovered that the yield of magic states can be further improved through the use of adaptive circuits, where circuit elements are adjusted based on mid-circuit measurements. This adaptive approach is a critical feature for various error-correction subroutines, showcasing the versatility and capabilities of the proposed methodology. The implications of this research are significant for the future of quantum computing, as the developed prototype offers a promising solution to reduce the number of physical qubits required to generate high-fidelity magic states in large-scale quantum-computing architectures. By leveraging error correction and adaptive techniques, this study represents a major milestone in advancing the field of quantum computing and paves the way for the realization of efficient and reliable quantum algorithms on a larger scale.